Partial Derivative

Partial Derivative Definition: 

Partial derivatives are defined as derivatives of a function of multiple variables when all but the variable of interest is held fixed during the differentiation.  

Let f(x,y) be a function with two variables. If we keep y constant and differentiate f (assuming f is differentiable) with respect to the variable x, using the rules and formulas of differentiation, we obtain what is called the partial derivative of ‘f’ with respect to x which is denoted by 

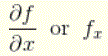
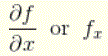
Similarly, If we keep x constant and differentiate f (assuming f is differentiable) with respect to the variable y, we obtain what is called the  

 partial derivative of ‘f’ with respect to y which is denoted by 

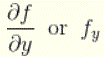
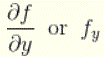
Examples: 

Example# 1: 

Find the partial derivatives f_x and f_y if f(x , y) is given by 

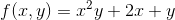
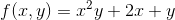
Solution of example# 1: 

Assume ‘y’ is constant and differentiate with respect to x to obtain 
 

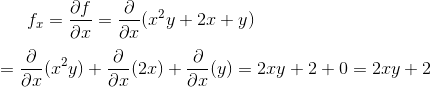
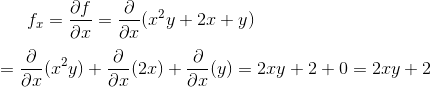
Now assume x is constant and differentiate with respect to y to obtain 

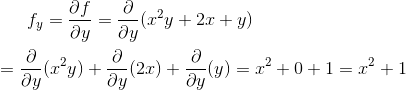
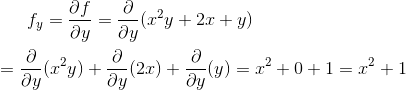
Example# 2: 

Find f_x and f_y if f(x , y) is given by 

 
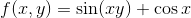
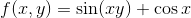
Solution to Example 2: 
Differentiate with respect to x assuming y is constant 

 
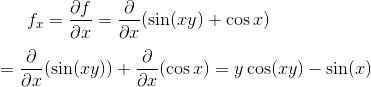
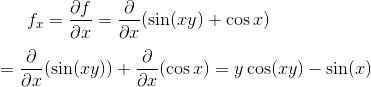
Differentiate with respect to y assuming x is constant 

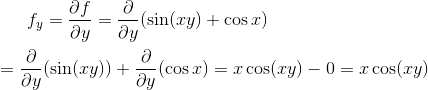
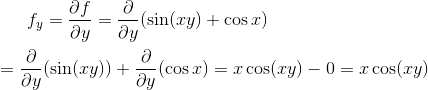
Example# 3: 

Find f_x and f_y if f(x , y) is given by 

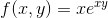
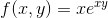
Solution to Example 3: 
Differentiate with respect to x assuming y is constant using the product rule of differentiation. 
 

 
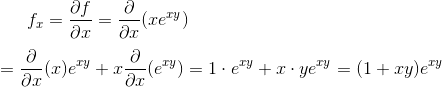
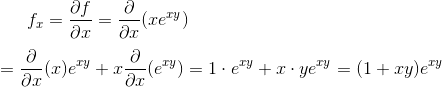
Differentiate with respect to y assuming x is constant. 

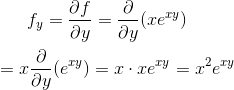
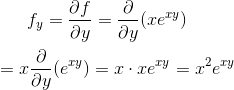
Example# 4: 

Find f_x and f_y if f(x , y) is given by 

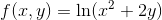
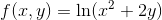
Solution to Example 4: 
Differentiate with respect to x to obtain 

 
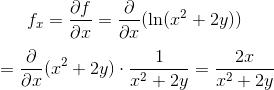
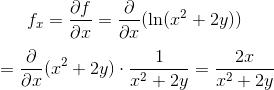
Differentiate with respect to y 

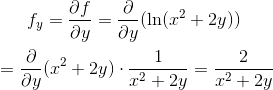
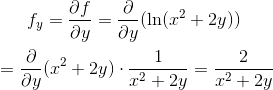
Example# 5: 

Find f_x(2 , 3) and f_y(2 , 3) if f(x , y) is given by 

 
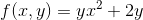
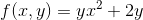
Solution to Example 5: 
We first find the partial derivatives f_x and f_y 
fx(x,y) = 2x y 
f_y(x,y) = x² + 2 
We now calculate f_x(2 , 3) and f_y(2 , 3) by substituting x and y by their given values 
f_x(2,3) = 2 (2)(3) = 12 
f_y(2,3) = 2² + 2 = 6 

Phrasing and notation 

Here are some of the phrases you might hear in reference to ∂f /∂f operation: 

• “The partial derivative of ‘ with respect to ” 

• “Del f, del x” 
• “Partial f, partial x” 
• “The partial derivative (of ‘) in the ‘-direction” 

Alternate notation: 

In the same way that people sometimes prefer to write f ′ instead of d f / d x, we have the following notation: 

          fx ↔∂x/∂f  

         fy ↔ ∂f/ ∂y 

       F(some variable)  ↔ ∂f/ ∂ (That same variable) 

A more formal definition: 

Although thinking of dx or ∂x as really tiny changes in the value of x is a useful intuition, it is healthy to occasionally step back and remember that defining things precisely requires introducing limits. After all, what specific small value would ∂x be? One one hundredth? One one millionth? 10^10^10? 

The point of calculus is that we don’t use any one tiny number, but instead consider all possible values and analyze what tends to happen as they approach a limiting value. The single variable derivative, for example, is defined like this: 

dx/df (x0) = h→0lim       ( hf (x0 +h)−f(x0 ))  / h 

• h represents the “tiny value” that we intuitively think of as dx. 
• The h→0 under the limit indicates that we care about very small values of h, those approaching 0. 
• f(x0 +h)−f(x0 ) is the change in the output that results from adding h to the input, which is what we think of as df.  

Formally defining the partial derivative looks almost identical. If x,y…), is a function with multiple inputs, here’s how that looks: 

∂x / ∂f  (x0 ,y0 ,…)  = h→0lim (hf (x0 +h, y0  ,…) − f (x0 ,y0 ,…))   /h  

The point is that h, which represents a tiny tweak to the input, is added to different input variables depending on which partial derivative we are taking. 

People will often refer to this as the limit definition of a partial derivative. 

You may be interested in Matrix Determinant Calculator.

Second Partial Derivative:  

A brief overview of second partial derivative, the symmetry of mixed partial derivatives, and higher order partial derivatives. 

Notations of Second Order Partial Derivatives: 

 For a two variable function f(x , y), we can define 4 second order partial derivatives along with their notations. 

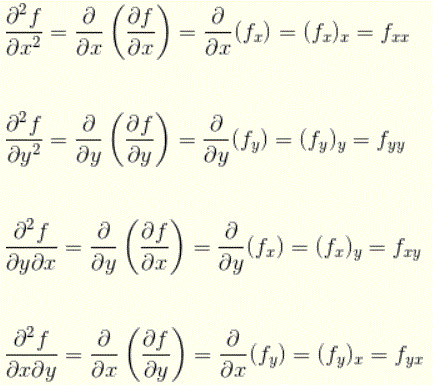
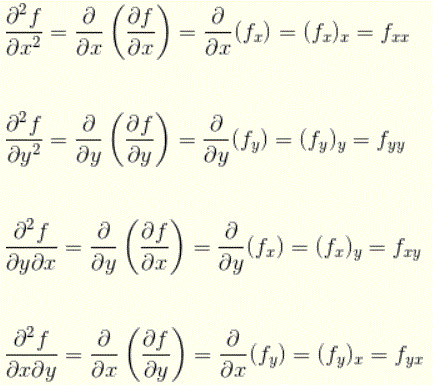
Examples with Detailed solutions: 

Example# 1 
Find f_xx, f_yy given that f(x , y) = sin (x y) 
Solution: 
f_xx may be calculated as follows: 
f_xx = ∂²f / ∂x² = ∂(∂f / ∂x) / ∂x 
= ∂(∂[ sin (x y) ]/ ∂x) / ∂x 
= ∂(y cos (x y) ) / ∂x 
= – y² sin (x y) ) 
f_yy can be calculated as follows: 
f_yy = ∂²f / ∂y² = ∂(∂f / ∂y) / ∂y 
= ∂(∂[ sin (x y) ]/ ∂y) / ∂y 
= ∂(x cos (x y) ) / ∂y 
= – x² sin (x y)  

Example# 2 
Find f_xx, f_yy, f_xy, f_yx given that f(x , y) = x³ + 2 x y. 
Solution: 
f_xx is calculated as follows: 
f_xx = ∂²f / ∂x² = ∂(∂f / ∂x) / ∂x 
= ∂(∂[ x³ + 2 x y ]/ ∂x) / ∂x 
= ∂( 3 x² + 2 y ) / ∂x 
= 6x 
f_yy is calculated as follows: 
f_yy = ∂²f / ∂y² = ∂(∂f / ∂y) / ∂y 
= ∂(∂[ x³ + 2 x y ]/ ∂y) / ∂y 
= ∂( 2x ) / ∂y 
= 0 
f_xy is calculated as follows: 
f_xy = ∂²f / ∂y∂x = ∂(∂f / ∂x) / ∂y 
= ∂(∂[ x³ + 2 x y ]/ ∂x) / ∂y 
= ∂( 3 x² + 2 y ) / ∂y 
= 2 
f_yx is calculated as follows: 
f_yx = ∂²f / ∂x∂y = ∂(∂f / ∂y) / ∂x 
= ∂(∂[ x³ + 2 x y ]/ ∂y) / ∂x 
= ∂( 2x ) / ∂x 
= 2 

Example# 3 
Find f_xx, f_yy, f_xy, f_yx given that f(x , y) = x³y⁴ + x² y. 
Solution: 
f_xx is calculated as follows: 
f_xx = ∂²f / ∂x² = ∂(∂f / ∂x) / ∂x 
= ∂(∂[ x³y⁴ + x² y ]/ ∂x) / ∂x 
= ∂( 3 x²y⁴ + 2 x y) / ∂x 
= 6x y⁴ + 2y 
f_yy is calculated as follows: 
f_yy = ∂²f / ∂y² = ∂(∂f / ∂y) / ∂y 
= ∂(∂[ x³y⁴ + x² y ]/ ∂y) / ∂y 
= ∂( 4 x³y³ + x² ) / ∂y 
= 12 x³y^2 
f_xy is calculated as follows: 
f_xy = ∂²f / ∂y∂x = ∂(∂f / ∂x) / ∂y 
= ∂(∂[ x³y⁴ + x² y ]/ ∂x) / ∂y 
= ∂( 3 x²y⁴ + 2 x y ) / ∂y 
= 12 x²y³ + 2 x 
f_yx is calculated as follows: 
f_yx = ∂²f / ∂x∂y = ∂(∂f / ∂y) / ∂x 
= ∂(∂[ x³y⁴ + x² y ]/ ∂y) / ∂x 
= ∂(4 x³y³ + x²) / ∂x 
= 12 x²y³ + 2x 

The gradient 

The gradient stores all the partial derivative information of a multivariable function.  But it’s more than a mere storage device, it has several wonderful interpretations and many, many uses. 

Example: 

The gradient of a function f, denoted as ∇f, is the collection of all its partial derivatives into a vector. This is most easily understood with an example. 

Let f(x,y)= x^2y. Find ∇f(3,2). 

Solution:  The gradient is just the vector of partial derivatives. The partial derivatives of f, at the point (x,y)=(3,2) are: 

∂f/∂x (x,y) = 2xy    

∂f/∂x (3,2) = 12 

∂f/∂y (x,y) = x2 

∂f/∂y (3,2) = 9 

Therefore, the gradient is 

∇f(3,2) = 12i+9j = (12,9).