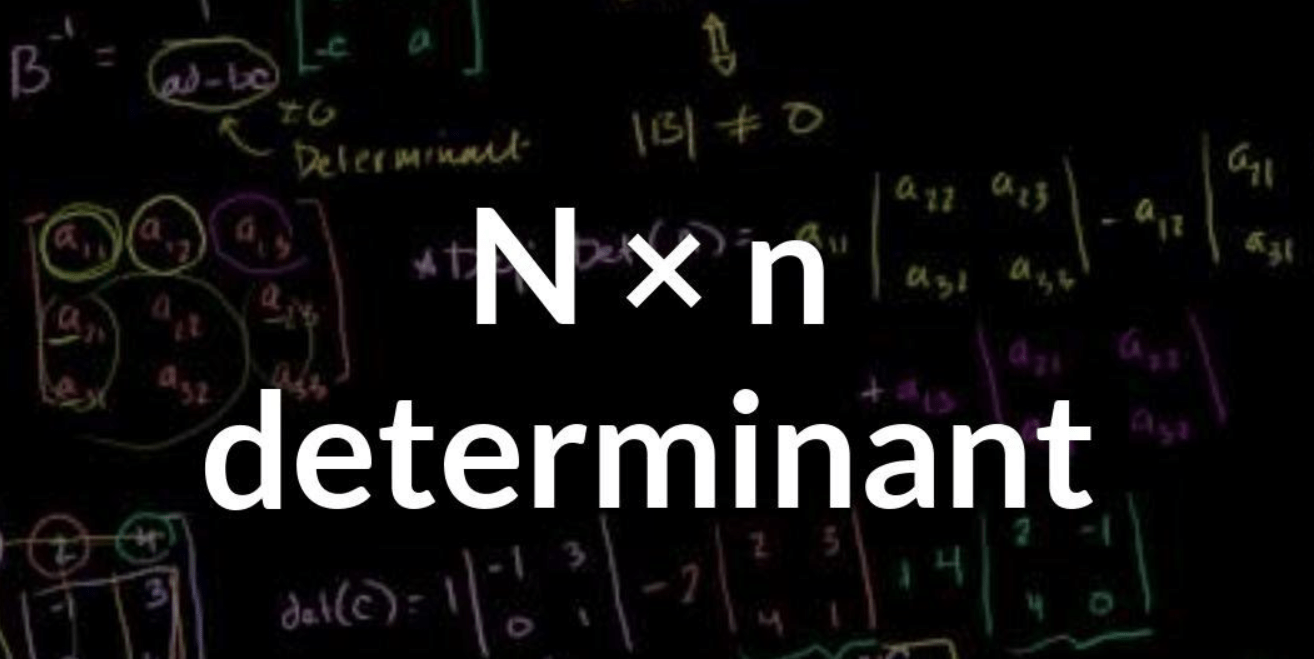Determinant calculator can be automatic or manual. In automatic calculators, you may put values and get answer, but you will not be able to learn. Therefore, in this procedure, we will teach you manual determinant calculator method to understand step by step.
Determinant is considered an algebraic representation of the sum of the products of elements each with an algebraic symbol, typically in a square array and used for the solution of systems of linear equations.
The determinant for linear algebra is a scalar value that can be determined by square matrix elements and which encodes those linear transformation properties defined in a matrix. The determinant of a matrix A is denoted det(A), det A, or |A|.
The volume scaling factor defined in the matrix can be considered geometrically as the linear transformation. This is also the signed n-dimensional volume occupied by the matrix ‘ column or row vectors. The determinant is either positive or negative based on the preservation or reversal of n-space orientation through the linear mapping.
In the case of a 2 × 2 matrix the determinant calculator may be defined as:
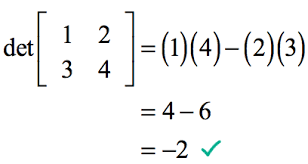
In the cast of 3×3 matrix, the determinant calculator may be defined as:
Now, it is time to go through the types of determinant matrixes.
Table of Contents
2×2 Matrices:
What is a 2×2 matrix?
A matrix that contains two rows and two columns is known as 2x2matrix. A 2X2 matrix is a tool used to help gain insight and outcomes in a dialogue. On each end of the spectrum designers create a matrix of 2×2 with opposite features (i.e. cheap versus costly).
Why to use a 2×2 matrix?
A 2×2 matrix is a tool that allows people to think and talk about issues. Use it to help you learn about connections between things or people during your synthesis process. It is expected that a 2×2 will provide input. 2×2 matrices are perfect for expressing a reference you want to communicate visually.
You may be interested in reading more articles on Learn Cybers.
How to use a 2×2 matrix?
For a 2×2 matrix (2 rows and 2 columns):
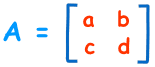
The determinant is:
|A| = ad − bc
“The determinant of A equals a times d minus b times c”
If the input in the matrix is real, Matrix A can be used in two linear maps: One, which maps the regular base vectors to A rows, and the other, which maps them to A columns- A. In other words, you subtract the top-to-bottom-right diagonal to take the determinants of a 2-2 matrix, from which you extract the product from the bottom-left-to-top-right diagonal.
It is easy to remember when you think of a cross:
- Blue is positive (+ad),
- Red is negative (−bc)
Example-1:
Find determinant of the following matrix ‘B’:
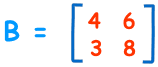
|B|= 4×8 − 6×3
= 32−18
= 14
Inverse of a 2×2 matrix:
So, how to calculate the inverse of a 2×2 matrix?
It’s very easy. For a 2×2 matrix:

In other words; switch the positions of a and d, put negatives on b and c, and split all by evaluating (ad-bc). Just for example:
Example-2:
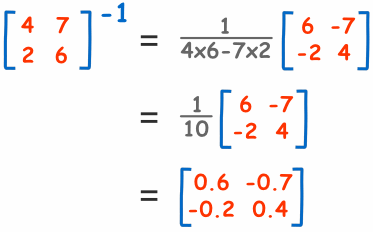
For your kind information:
it must be true that: A × A-1 = I
You may be interested in reading more articles on Learn Cybers.
Multiplication of a 2×2 matices:
That row of the first matrix is taken and every column of the second matrix is multiplied. Together, that contributes. And after that, find the determinant of that resulted matrix.
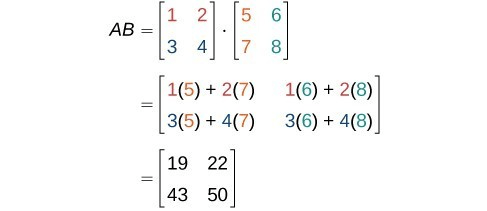
3×3 Matrix:
A matrix that contains three rows and three columns is known as 3×3 matrix.
How to find/solve a 3×3 matrix?
The traditional method for calculating a matrix of 3×3 is a breakdown of smaller, easy-to-manage, evaluating problems of 2×2.
For Example-1:
For a 3×3 matrix:
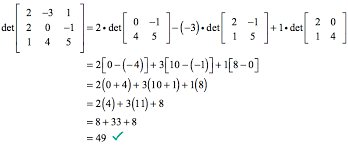
Inverse of a 3×3 matrix:
Here, we have used Elementary Row operation for finding the inverse of a 3×3 matrix.
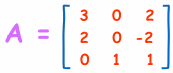
We begin with matrix A and write it down next to it with an identity matrix I:


(This is called the “Augmented Matrix”)
Here, ’I’ is known as Identity Matrix.
Sponsored by WebSoft IT Development Solutions (Private) Limited
Identity Matrix:
The “Identity Matrix” is the matrix equivalent of the number “1”:
A 3×3 Identity Matrix
- It is “square” (has same number of rows as columns),
- It has 1s on the diagonal and 0s everywhere else.
- It’s symbol is the capital letter I.
But in Elementary Row Operation, we can only do,
- swap rows
- multiply or divide each element in a a row by a constant
- replace a row by adding or subtracting a multiple of another row to it
We do these steps as follows:
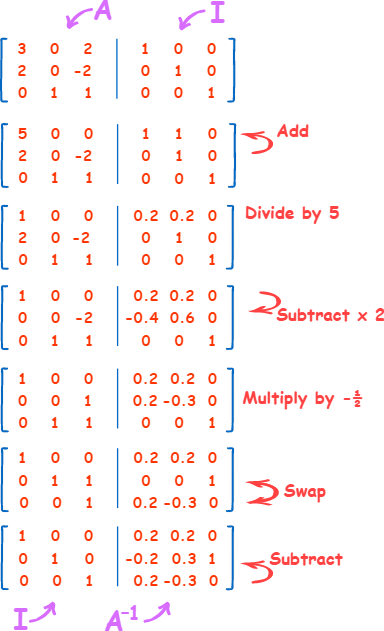
No.1- Start with A next to I
No.2- Add row 2 to row 1,
No.3- then divide row 1 by 5,
No.4- Then take 2 times the first row, and subtract it from the second row,
No.5- Multiply the second row by -1/2,
No.6- Now swap the second and third row,
No.7- Last, subtract the third row from the second row,
And we are done!
And matrix A has been made into an Identity Matrix and at the same time an Identity Matrix got made into A-1.
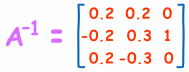
Multiplication of 3×3 matrix:
The following example explains the multiplication of two 3×3 matixes.
Example-1:
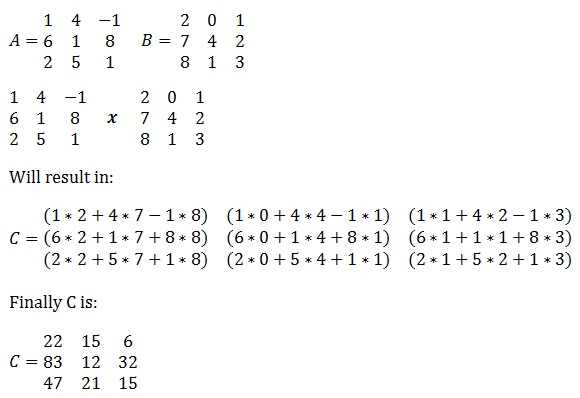
Then find the determinant of the resulted matrix ‘C’, by using the method that is explained earlier.
4×4 Matrix:
A matrix having four rows and four columns is known as 4×4 matrix. E.g:this is a 4×4 matrix.
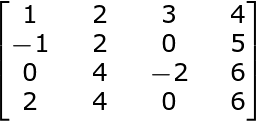
The inverse of a 4×4 matrix:
The following is the easiest formula that shows the way of finding the inverse of a 4×4 matrix;
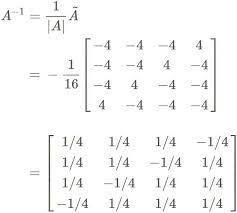
Using this formula, you can easily find the determinant of a 4×4 matrix by applying the determinant formula to the resulted matrix.
You may be interested in reading more articles on Learn Cybers.
Applications of determinants:
Following are the applications of a determinant:
- Linear Independence
- The orientation of a basis
- Volume and Jacobean Determinant
- Vandermonde Determinant
- Circulants