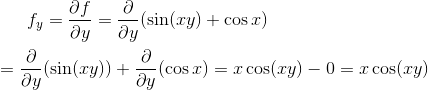Definition:

Partial derivatives are defined as derivatives of multiple variables when they are fixed during the differentiation, except for the variable of interest.

Let f(x, y) be a two-variable function. If we maintain and differentiate f in relation to the variable x (assuming that f is differentiable), using the rules and formulas for differentiation, we get what is called the’ f’ partial derivative for x that is denoted by

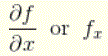
Similar to this we can obtain the so-called partial “f” derivative, which is indicated by Y if we keep x constant and differentiate f with regard to variable y.

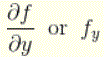
Examples:

Problem 1:

Find fx and fy partial derivatives if f(x, y) is specified as:

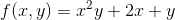
Solution:

Suppose that ‘ y ‘ is constant in order to obtain x:

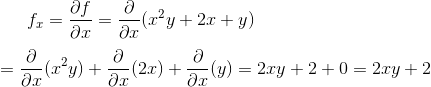
Now assume x is constant and differentiate with respect to y to obtain:

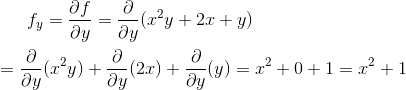
Problem 2:

Find f_x and f_y if f(x , y) is given by

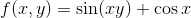
Solution:

Differentiate with respect to x assuming y is constant:

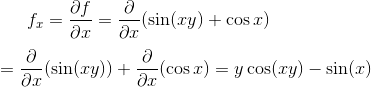
Differentiate with respect to y assuming x is constant