Table of Contents
Partial Derivative Definition:
Partial derivatives are defined as derivatives of a function of multiple variables when all but the variable of interest is held fixed during the differentiation.
Let f(x,y) be a function with two variables. If we keep y constant and differentiate f (assuming f is differentiable) with respect to the variable x, using the rules and formulas of differentiation, we obtain what is called the partial derivative of ‘f’ with respect to x which is denoted by
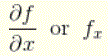
Similarly, If we keep x constant and differentiate f (assuming f is differentiable) with respect to the variable y, we obtain what is called the
partial derivative of ‘f’ with respect to y which is denoted by
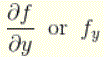
Examples:
Example# 1:
Find the partial derivatives fx and fy if f(x , y) is given by
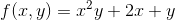
Solution of example# 1:
Assume ‘y’ is constant and differentiate with respect to x to obtain
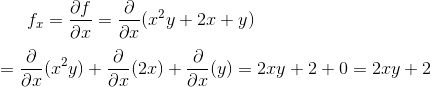
Now assume x is constant and differentiate with respect to y to obtain
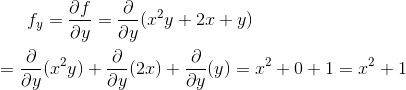
Example# 2:
Find fx and fy if f(x , y) is given by
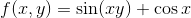
Solution to Example 2:
Differentiate with respect to x assuming y is constant
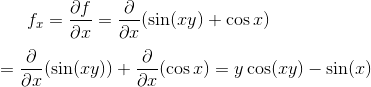
Differentiate with respect to y assuming x is constant
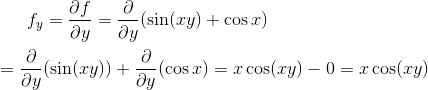
Example# 3:
Find fx and fy if f(x , y) is given by
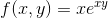
Solution to Example 3:
Differentiate with respect to x assuming y is constant using the product rule of differentiation.
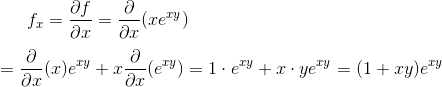
Differentiate with respect to y assuming x is constant.
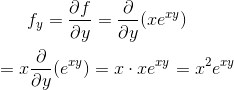
Example# 4:
Find fx and fy if f(x , y) is given by
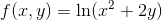
Solution to Example 4:
Differentiate with respect to x to obtain
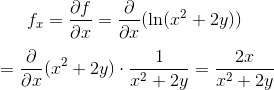
Differentiate with respect to y
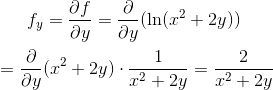
Example# 5:
Find fx(2 , 3) and fy(2 , 3) if f(x , y) is given by
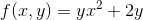
Solution to Example 5:
We first find the partial derivatives fx and fy
fx(x,y) = 2x y
fy(x,y) = x2 + 2
We now calculate fx(2 , 3) and fy(2 , 3) by substituting x and y by their given values
fx(2,3) = 2 (2)(3) = 12
fy(2,3) = 22 + 2 = 6
Phrasing and notation
Here are some of the phrases you might hear in reference to ∂f /∂f operation:
- “The partial derivative of ‘ with respect to ”
- “Del f, del x”
- “Partial f, partial x”
- “The partial derivative (of ‘) in the ‘-direction”
Alternate notation:
In the same way that people sometimes prefer to write f ′ instead of d f / d x, we have the following notation:
fx ↔∂x/∂f
fy ↔ ∂f/ ∂y
F(some variable) ↔ ∂f/ ∂ (That same variable)
A more formal definition:
Although thinking of dx or ∂x as really tiny changes in the value of x is a useful intuition, it is healthy to occasionally step back and remember that defining things precisely requires introducing limits. After all, what specific small value would ∂x be? One one hundredth? One one millionth? 10^10^10?
The point of calculus is that we don’t use any one tiny number, but instead consider all possible values and analyze what tends to happen as they approach a limiting value. The single variable derivative, for example, is defined like this:
dx/df (x0) = h→0lim ( hf (x0 +h)−f(x0 )) / h
- h represents the “tiny value” that we intuitively think of as dx.
- The h→0 under the limit indicates that we care about very small values of h, those approaching 0.
- f(x0 +h)−f(x0 ) is the change in the output that results from adding h to the input, which is what we think of as df.
Formally defining the partial derivative looks almost identical. If x,y…), is a function with multiple inputs, here’s how that looks:
∂x / ∂f (x0 ,y0 ,…) = h→0lim (hf (x0 +h, y0 ,…) − f (x0 ,y0 ,…)) /h
The point is that h, which represents a tiny tweak to the input, is added to different input variables depending on which partial derivative we are taking.
People will often refer to this as the limit definition of a partial derivative.
You may be interested in Matrix Determinant Calculator.
Second Partial Derivative:
A brief overview of second partial derivative, the symmetry of mixed partial derivatives, and higher order partial derivatives.
Notations of Second Order Partial Derivatives:
For a two variable function f(x , y), we can define 4 second order partial derivatives along with their notations.
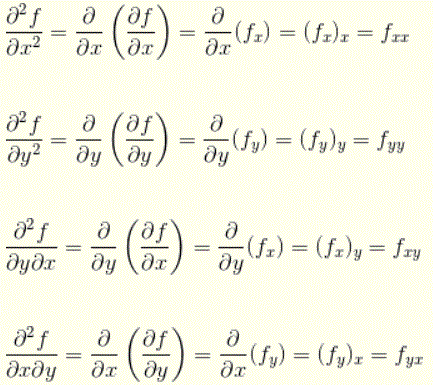
Examples with Detailed solutions:
Example# 1
Find fxx, fyy given that f(x , y) = sin (x y)
Solution:
fxx may be calculated as follows:
fxx = ∂2f / ∂x2 = ∂(∂f / ∂x) / ∂x
= ∂(∂[ sin (x y) ]/ ∂x) / ∂x
= ∂(y cos (x y) ) / ∂x
= – y2 sin (x y) )
fyy can be calculated as follows:
fyy = ∂2f / ∂y2 = ∂(∂f / ∂y) / ∂y
= ∂(∂[ sin (x y) ]/ ∂y) / ∂y
= ∂(x cos (x y) ) / ∂y
= – x2 sin (x y)
Example# 2
Find fxx, fyy, fxy, fyx given that f(x , y) = x3 + 2 x y.
Solution:
fxx is calculated as follows:
fxx = ∂2f / ∂x2 = ∂(∂f / ∂x) / ∂x
= ∂(∂[ x3 + 2 x y ]/ ∂x) / ∂x
= ∂( 3 x2 + 2 y ) / ∂x
= 6x
fyy is calculated as follows:
fyy = ∂2f / ∂y2 = ∂(∂f / ∂y) / ∂y
= ∂(∂[ x3 + 2 x y ]/ ∂y) / ∂y
= ∂( 2x ) / ∂y
= 0
fxy is calculated as follows:
fxy = ∂2f / ∂y∂x = ∂(∂f / ∂x) / ∂y
= ∂(∂[ x3 + 2 x y ]/ ∂x) / ∂y
= ∂( 3 x2 + 2 y ) / ∂y
= 2
fyx is calculated as follows:
fyx = ∂2f / ∂x∂y = ∂(∂f / ∂y) / ∂x
= ∂(∂[ x3 + 2 x y ]/ ∂y) / ∂x
= ∂( 2x ) / ∂x
= 2
Example# 3
Find fxx, fyy, fxy, fyx given that f(x , y) = x3y4 + x2 y.
Solution:
fxx is calculated as follows:
fxx = ∂2f / ∂x2 = ∂(∂f / ∂x) / ∂x
= ∂(∂[ x3y4 + x2 y ]/ ∂x) / ∂x
= ∂( 3 x2y4 + 2 x y) / ∂x
= 6x y4 + 2y
fyy is calculated as follows:
fyy = ∂2f / ∂y2 = ∂(∂f / ∂y) / ∂y
= ∂(∂[ x3y4 + x2 y ]/ ∂y) / ∂y
= ∂( 4 x3y3 + x2 ) / ∂y
= 12 x3y2
fxy is calculated as follows:
fxy = ∂2f / ∂y∂x = ∂(∂f / ∂x) / ∂y
= ∂(∂[ x3y4 + x2 y ]/ ∂x) / ∂y
= ∂( 3 x2y4 + 2 x y ) / ∂y
= 12 x2y3 + 2 x
fyx is calculated as follows:
fyx = ∂2f / ∂x∂y = ∂(∂f / ∂y) / ∂x
= ∂(∂[ x3y4 + x2 y ]/ ∂y) / ∂x
= ∂(4 x3y3 + x2) / ∂x
= 12 x2y3 + 2x
The gradient
The gradient stores all the partial derivative information of a multivariable function. But it’s more than a mere storage device, it has several wonderful interpretations and many, many uses.

Example:
The gradient of a function f, denoted as ∇f, is the collection of all its partial derivatives into a vector. This is most easily understood with an example.
Let f(x,y)= x^2y. Find ∇f(3,2).
Solution: The gradient is just the vector of partial derivatives. The partial derivatives of f, at the point (x,y)=(3,2) are:
∂f/∂x (x,y) = 2xy
∂f/∂x (3,2) = 12
∂f/∂y (x,y) = x2
∂f/∂y (3,2) = 9
Therefore, the gradient is
∇f(3,2) = 12i+9j = (12,9).

