We covered nearly 50 + primary Java interview questions in this tutorial for fresh and experienced candidates.
Table of Contents
Q.1- What is Java?
Java is a high-level programming language and is platform-independent. Java is a collection of objects. It was developed by Aun Microsystems. There are a lot of applications, websites and games that are developed using Java.
Q.2- What are features of Java?
The following are the features of Java:
OOP Concepts:
- Object-Oriented
- Inheritance
- Encapsulation
- Polymorphism
- Abstraction
Other Concepts:
- Platform independent: A single program works on different platforms without any modification.
- High Performance: JIT (Just In Time compiler) enables high performance in Java. JIT converts the bytecode into machine language and then JVM starts the execution.
- Multi-threaded: A flow of execution is known as a Thread. JVM creates a thread which is called main thread. The user can create multiple threads by extending the thread class or by implementing Runnable interface.
Q.3- How does Java enable high performance?
To enable high-performance, Java uses just in time compilers. JIT is used for byte coding of the instructions.
Q.4- What are the Java IDEs?
Eclipse and NetBeans are the IDEs of Java.
Q.5- What do you mean by Constructor?
The following points will explain the Constructor in detail:
- A constructor is called up according to the class when a new object is installed on a program.
- The builder is a process with the same name as the name of the unit.
- A default builder will be created if a user does not construct a builder implicitly.
- You can overload the manufacturer.
- Once a builder with a parameter is created, the user will specifically create a builder with no parameter.
Q.6- What is meant by the Local variable and Instance variable?
Local variables are defined in the method and scope of variables that have existed inside the method itself.
An instance variable is defined inside the class and outside the method and scope of variables exist throughout the class.
Q.7- What is a class?
The class is the definition of all Java codes. A class has different parameters and methods.
Variables are attributes that define the class status.
Methods is the exact location for carrying out business logic. It contains a set of declarations (or) to fulfil the specific requirement.
Q.8- What is an Object?
An instance of a class is called object. The object has state and behaviour.
Whenever the JVM reads the “new()” keyword then it will create an instance of that class.
Q.9- What are the OOP concepts?
The OOP concepts include:
- Inheritance
- Encapsulation
- Polymorphism
- Abstraction
- Interface
Q.10- What is Inheritance?
Inheritance means one class can extend to another class. So that the codes can be reused from one class to another class.
Existing class is known as Super class whereas the derived class is known as a sub class.
Example:
Super class:
public class Manipulation{
}Sub class:
public class Addition extends Manipulation{
}Inheritance is applicable for public and protected members only. Private members can’t be inherited.
Q.11- What is Encapsulation?
Purpose of Encapsulation:
- Protects the code from others.
- Code maintainability.
Example:
We are declaring ‘a’ as an integer variable and it should not be negative.
public class{
int a=5;
}If someone changes the exact variable as “a = -5” then it is bad.
In order to overcome the problem, we need to follow the below steps:
- We can make the variable as private or protected one.
- Use public accessor methods such as set<property> and get<property>.
So that the above code can be modified as:
public class Addition{
private int a = 5; //Here the variable is marked as private
} Below code shows the getter and setter.
Conditions can be provided while setting the variable.
get A{
}
set A(int a){
if(a>0){
// Here condition is applied
}
}We need to render all the instance variables as private for encapsulation and build setter and getter for those variables. Which in effect will cause others to call the setters instead of directly accessing the data.
Q.12- What is Polymorphism?
Polymorphism means many forms.
A single object can refer to the super class or sub-class depending on the reference type which is called polymorphism.
Example:
public class Manipulation{
//Super class
public void add(){
}
}
public class Addition extends Manipulation(){
// Sub class
public void add(){
}
public static void main(String args[]){
//Manipulation is reference type and Addition is reference type
Manipulation addition = new Addition();
addition.add();
}
}Using Manipulation reference type we can call the Addition class “add()” method. This ability is known as Polymorphism.
Polymorphism is applicable for overriding and not for overloading.
Q.13- What is meant by Method Overriding?
Method overriding happens if the sub class method satisfies the below conditions with the Super class method:
- Method name should be same
- Argument should be same
- Return type also should be same
The key benefit of overriding is that the Sub class can provide some specific information about that sub class type than the super class.
Example:
public class Manipulation{
//Super class
public void add(){
}
}
public class Addition extends Manipulation{
public void add(){
}
public static void main(String args[]){
Manipulation addition = new Addition();
//Polymorphism is applied
addition.add();
// It calls the Sub class add() method
}
} addition.add() method calls the add() method in the Sub class and not the parent class. So it overrides the Super class method and is known as Method Overriding.
Q.14- What is Method Overloading?
Method overloading happens for different classes or within the same class.
For method overloading, subclass method should satisfy the below conditions with the Super class method (or) methods in the same class itself:
- Same method name
- Different argument type
- May have different return types
Example:
public class Manipulation{
//Super class
public void add(String name){
//String parameter
}
}
public class Addition extends Manipulation(){
public void add(){
//No Parameter
}
public void add(int a){
//integer parameter
}
public static void main(String args[]){
Addition addition = new Addition();
addition.add();
}
} Here the add() method having different parameters in the Addition class is overloaded in the same class as well as with the super class.
Note: Polymorphism is not applicable for method overloading.
Q.15- What is Interface in Java?
Multiple inheritance cannot be achieved in java. To overcome this problem Interface concept is introduced.
An interface is a template which has only method declarations and not the method implementation.
Example:
public abstract interface IManupulation{
//Interface declaration
public abstract void add(); //method declaration
public abstract void subtract();
} - All the methods in the interface are internally public abstract void.
- All the variables in the interface are internally public static final that is constants.
- Classes can implement the interface and not extends.
- The class which implements the interface should provide an implementation for all the methods declared in the interface.
public class Manupulation implements IManupulation{
//Manupulation class uses the interface
public void add(){
}
public void subtract(){
}
}Q.16- What is Abstract class in Java?
We can create the Abstract class by using “Abstract” keyword before the class name. An abstract class can have both “Abstract” methods and “Non-abstract” methods that are a concrete class.
Abstract method:
The method which has only the declaration and not the implementation is called the abstract method and it has the keyword called “abstract”. Declarations are the ends with a semicolon.
Example:
public abstract class Manupulation{
public abstract void add(); //Abstract method declaration
public void subtract(){
}
}- An abstract class may have a Non- abstract method also.
- The concrete Subclass which extends the Abstract class should provide the implementation for abstract methods.
Q.17- Difference between Array and Array List.
The Difference between Array and Array List can be understood from the below table:
| Array | Array List |
| Size should be given at the time of array declaration. String[] name = new String[2] | Size may not be required. It changes the size dynamically. ArrayList name = new ArrayList |
| To put an object into array we need to specify the index. name[1] = “book” | No index required. name.add(“book”) |
| Array is not type parameterized | ArrayList in java 5.0 are parameterized. Eg: This angle bracket is a type parameter which means a list of String. |
Q.18- Difference between String, String Builder, and String Buffer.
String: String variables are stored in “constant string pool”. Once the string reference changes the old value that exists in the “constant string pool”, it cannot be erased.
Example:
String name = “book”;
Constant string pool
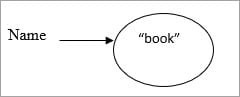
.
If the name value has changed from “book” to “pen”.
Constant string pool
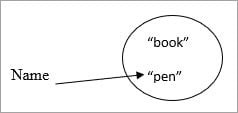
Then the older value retains in the constant string pool.
String Buffer:
- Here string values are stored in a stack. If the values are changed then the new value replaces the older value.
- The string buffer is synchronized which is thread-safe.
- Performance is slower than the String Builder.
Example:
String Buffer name =”book”;

Once the name value has been changed to “pen” then the “book” is erased in the stack.
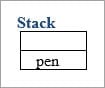
String Builder:
This is same as String Buffer except for the String Builder which is not threaded safety that is not synchronized. So obviously performance is fast.
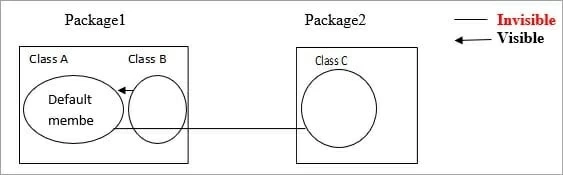
Q.19- Explain about Public and Private access specifiers.
Methods and instance variables are known as members.
Public:
Public members are visible in the same package as well as the outside package that is for other packages.
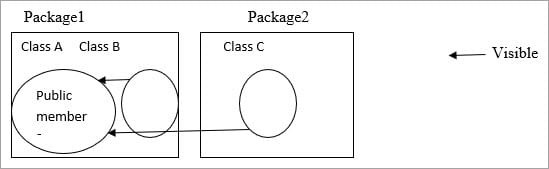
Public members in Class A are visible to Class B (Same package) as well as Class C (Different package).
Private:
Private members are visible in the same class only and not for the other classes in the same package as well as classes in the outside packages.
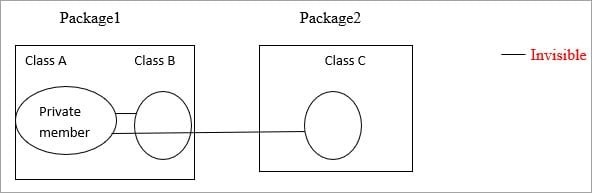
Private members in class A is visible only in that class. It is invisible for class B as well as class C.
Q.20- Difference between Default and Protected access specifiers.
Default: Methods and variables declared in a class without any access specifiers are called default.
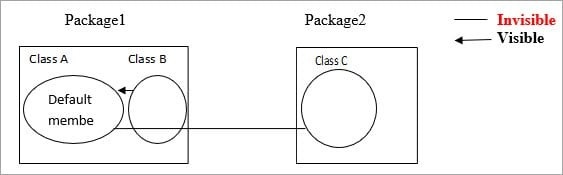
Default members in Class A are visible to the other classes which are inside the package and invisible to the classes which are outside the package.
So Class A members are visible to the Class B and invisible to the Class C.
Protected:
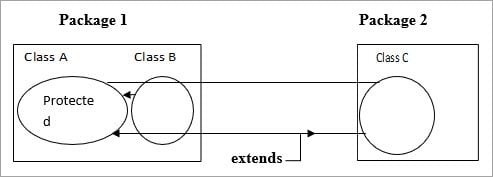
.
Protected is same as Default but if a class extends then it is visible even if it is outside the package.
Class A members are visible to Class B because it is inside the package. For Class C it is invisible but if Class C extends Class A then the members are visible to the Class C even if it is outside the package.
Q.21- Difference between HashMap and HashTable.
Difference between HashMap and HashTable can be seen below:
| HashMap | HashTable |
| Methods are not synchronized | Key methods are synchronized |
| Not thread safety | Thread safety |
| Iterator is used to iterate the values | Enumerator is used to iterate the values |
| Allows one null key and multiple null values | Doesn’t allow anything that is null |
| Performance is high than HashTable | Performance is slow |
Q.22- Difference between HashSet and TreeSet.
Difference between HashSet and TreeSet can be seen below:
| HashSet | TreeSet |
| Inserted elements are in random order | Maintains the elements in the sorted order |
| Can able to store null objects | Couldn’t store null objects |
| Performance is fast | Performance is slow |
Q.23- Difference between Abstract class and Interface.
Difference between Abstract Class and Interface are as follows:
Abstract Class:
- Abstract classes have a default constructor and it is called whenever the concrete subclass is instantiated.
- Contains Abstract methods as well as Non-Abstract methods.
- The class which extends the Abstract class shouldn’t require implementing all the methods, only Abstract methods need to be implemented in the concrete sub-class.
- Abstract Class contains instance variables.
Interface:
- Doesn’t have any constructor and couldn’t be instantiated.
- Abstract method alone should be declared.
- Classes which implement the interface should provide the implementation for all the methods.
- The interface contains only constants.
Q.24- What are Collections in Java?
Collection is a framework that is designed to store the objects and manipulate the design to store the objects.
Collections are used to perform the following operations:
- Searching
- Sorting
- Manipulation
- Insertion
- Deletion
A group of objects is known as collections. All the classes and interfaces for collecting are available in Java utile package.
Q.25- What are all the Classes and Interfaces that are available in the collections?
Given below are the Classes and Interfaces that are available in Collections:
Interfaces:
- Collection
- List
- Set
- Map
- Sorted Set
- Sorted Map
- Queue
Classes:
- Lists:
- Array List
- Vector
- Linked List
Sets:
- Hash set
- Linked Hash Set
- Tree Set
Maps:
- Hash Map
- Hash Table
- Tree Map
- Linked Hashed Map
Queue:
- Priority Queue
Q.26- What is meant by Ordered and Sorted in collections?
Ordered:
It means the values that are stored in a collection is based on the values that are added to the collection. So, we can iterate the values from the collection in a specific order.
Sorted:
Sorting mechanism can be applied internally or externally so that the group of objects sorted in a particular collection is based on properties of the objects.
Values added to the list is based on the index position and it is ordered by index position. Duplicates are allowed.
Types of Lists are:
Array List:
- Fast iteration and fast Random Access.
- It is an ordered collection (by index) and not sorted.
- It implements Random Access Interface.
Example:
public class Fruits {
public static void main(String[] args) {
ArrayList < String > names = new ArrayList < String > ();
names.add(“apple”);
names.add(“cherry”);
names.add(“kiwi”);
names.add(“banana”);
names.add(“cherry”);
System.out.println(names);
}
}Output:
[Apple, cherry, kiwi, banana, cherry]
From the output, Array List maintains the insertion order and it accepts the duplicates. But not sorted.
Vector:
It is same as Array List.
- Vector methods are synchronized.
- Thread safety.
- It also implements the Random Access.
- Thread safety usually causes a performance hit.
Example:
public class Fruit {
public static void main(String[] args) {
Vector < String > names = new Vector < String > ();
names.add(“cherry”);
names.add(“apple”);
names.add(“banana”);
names.add(“kiwi”);
names.add(“apple”);
System.out.println(“names”);
}
}Output:
[cherry,apple,banana,kiwi,apple]
Vector also maintains the insertion order and accepts the duplicates.
Linked List:
- Elements are doubly linked to one another.
- Performance is slow than Array list.
- Good choice for insertion and deletion.
- In Java 5.0 it supports common queue methods peek( ), Pool ( ), Offer ( ) etc.
Example:
Output
[ banana,cherry,apple,kiwi,banana]
Maintains the insertion order and accepts the duplicates.
Q.28 Explain about Set and their types in a collection?
Set cares about uniqueness. It doesn’t allow duplications. Here “equals ( )” method is used to determine whether two objects are identical or not.
Hash Set:
- Unordered and unsorted.
- Uses the hash code of the object to insert the values.
- Use this when the requirement is “no duplicates and don’t care about the order”.
Example:
public class Fruit {
public static void main(String[] args) {
HashSet < String > names = new HashSet <= String > ();
names.add(“banana”);
names.add(“cherry”);
names.add(“apple”);
names.add(“kiwi”);
names.add(“banana”);
System.out.println(names);
}
}Output:
[banana, cherry, kiwi, apple]
Doesn’t follow any insertion order. Duplicates are not allowed.
Linked Hash set:
- An ordered version of the hash set is known as Linked Hash Set.
- Maintains a doubly-Linked list of all the elements.
- Use this when the iteration order is required.
Example:
public class Fruit {
public static void main(String[] args) {
LinkedHashSet < String > names = new LinkedHashSet < String > ();
names.add(“banana”);
names.add(“cherry”);
names.add(“apple”);
names.add(“kiwi”);
names.add(“banana”);
System.out.println(names);
}
}Output:
[banana, cherry, apple, kiwi]
Maintains the insertion order in which they have been added to the Set. Duplicates are not allowed.
Tree Set:
- It is one of the two sorted collections.
- Uses “Read-Black” tree structure and guarantees that the elements will be in ascending order.
- We can construct a tree set with the constructor by using a comparable (or) comparator.
Example:
public class Fruits {
public static void main(String[] args) {
TreeSet < String > names = new TreeSet < String > ();
names.add(“cherry”);
names.add(“banana”);
names.add(“apple”);
names.add(“kiwi”);
names.add(“cherry”);
System.out.println(names);
}
}Output:
[apple, banana, cherry, kiwi]
TreeSet sorts the elements in ascending order. And duplicates are not allowed.
Q 29). Explain about Map and their types.
Ans: Map cares about unique identifier. We can map a unique key to a specific value. It is a key/value pair. We can search a value, based on the key. Like set, Map also uses “equals ( )” method to determine whether two keys are same or different.
Hash Map:
- Unordered and unsorted map.
- Hashmap is a good choice when we don’t care about the order.
- It allows one null key and multiple null values.
Example:
Public class Fruit{Public static void main(String[ ] args){HashMap<Sting,String> names =new HashMap<String,String>( );names.put(“key1”,“cherry”);names.put (“key2”,“banana”);names.put (“key3”,“apple”);names.put (“key4”,“kiwi”);names.put (“key1”,“cherry”);System.out.println(names);} }
Output:
{key2 =banana, key1=cherry, key4 =kiwi, key3= apple}
Duplicate keys are not allowed in Map.
Doesn’t maintain any insertion order and is unsorted.
Hash Table:
- Like vector key, methods of the class are synchronized.
- Thread safety and therefore slows the performance.
- Doesn’t allow anything that is null.
Example:
public class Fruit{public static void main(String[ ]args){Hashtable<Sting,String> names =new Hashtable<String,String>( );names.put(“key1”,“cherry”);names.put(“key2”,“apple”);names.put(“key3”,“banana”);names.put(“key4”,“kiwi”);names.put(“key2”,“orange”);System.out.println(names);} }
Output:
{key2=apple, key1=cherry,key4=kiwi, key3=banana}
Duplicate keys are not allowed.
Linked Hash Map:
- Maintains insertion order.
- Slower than Hash map.
- Can expect a faster iteration.
Example:
public class Fruit{public static void main(String[ ] args){LinkedHashMap<Sting,String> names =new LinkedHashMap<String,String>( ); names.put(“key1”,“cherry”); names.put(“key2”,“apple”); names.put(“key3”,“banana”); names.put(“key4”,“kiwi”); names.put(“key2”,“orange”); System.out.println(names); } }
Output:
{key2=apple, key1=cherry,key4=kiwi, key3=banana}
Duplicate keys are not allowed.
TreeMap:
- Sorted Map.
- Like Tree set, we can construct a sort order with the constructor.
Example:
public class Fruit{public static void main(String[ ]args){TreeMap<Sting,String> names =new TreeMap<String,String>( );names.put(“key1”,“cherry”);names.put(“key2”,“banana”);names.put(“key3”,“apple”);names.put(“key4”,“kiwi”);names.put(“key2”,“orange”);System.out.println(names);}}
Output:
{key1=cherry, key2=banana, key3 =apple, key4=kiwi}
It is sorted in ascending order based on the key. Duplicate keys are not allowed.
Q.30- What is meant by Exception?
Ans- An Exception is an issue that can occur during an execution’s normal flow. When something wails at runtime, a method can throw an exception. If the exception can not be treated, the execution will be terminated before the task is completed.
If the exception is treated, the normal flow should proceed. Exceptions are java.lang.Exception subclasses.
Q.31- What are types of exception?
Ans- Two types of exceptions are described in detail below:
Checked Exception: At the time of compilation, the compiler tests certain exceptions. Classes that extend the Throwable class with the exception of Runtime and Error are called Exception Checked.
Checked Exceptions either have to announce the exception using keyword throes (or) followed by correct attempt / catch.
E.g. ClassNotFound Error Unchecked Exception: The compiler does not test such exceptions during the compilation period. Such exceptions are not treated by the compiler.
This includes: ArrayIndexOutOfBounds Error Arithmetic Exception.
Q.32- Explain the problem of priority.
Answer: Queue Interface
Priority Queue: In order to implement the queue application, the Linked list class has been improved. It is possible to manage the queues with a connected list. A queue’s function is “Priority-in, Priority-out.”
Elements are therefore ordered either naturally or in compliance with the comparator. The ordering of the elements is their relative priority.
Q.33- What are the different ways to handle exceptions?
Ans: Two different ways to handle exception are explained below:
#1) Using try/catch:
A risky code is surrounded by try block. If an exception occurs, then it is caught by the catch block which is followed by the try block.
Example:
| 1 | class Manipulation{ |
| 2 | public static void main(String[] args){ |
| 3 | add(); |
| 4 | } |
| 5 | Public void add(){ |
| 6 | try{ |
| 7 | addition(); |
| 8 | }catch(Exception e){ |
| 9 | e.printStacktrace(); |
| 10 | } |
| 11 | } |
| 12 | } |
#2) By declaring throws keyword:
At the end of the method, we can declare the exception using throws keyword.
Example:
| 1 | class Manipulation{ |
| 2 | public static void main(String[] args){ |
| 3 | add(); |
| 4 | } |
| 5 | public void add() throws Exception{ |
| 6 | addition(); |
| 7 | } |
| 8 | } |
Q.34- What are the Advantages of Exception handling?
Ans: Given below are the advantages:
- The normal flow of the execution won’t be terminated if exception got handled
- We can identify the problem by using catch declaration
Q.35- What are Exception handling keywords in Java?
Ans: Given below are the two Exception Handling Keywords:
try:
When a risky code is surrounded by a try block. An exception occurring in the try block is caught by a catch block. Try can be followed either by catch (or) finally (or) both. But any one of the blocks is mandatory.
catch:
This is followed by try block. Exceptions are caught here.
finally:
This is followed either by try block (or) catch block. This block gets executed regardless of an exception. So generally clean up codes are provided here.
are explained below:
#1) Using try/catch:
A risky code is surrounded by try block. If an exception occurs, then it is caught by the catch block which is followed by the try block.
Example:
| 1 | class Manipulation{ |
| 2 | public static void main(String[] args){ |
| 3 | add(); |
| 4 | } |
| 5 | Public void add(){ |
| 6 | try{ |
| 7 | addition(); |
| 8 | }catch(Exception e){ |
| 9 | e.printStacktrace(); |
| 10 | } |
| 11 | } |
| 12 | } |
#2) By declaring throws keyword:
At the end of the method, we can declare the exception using throws keyword.
Example:
| 1 | class Manipulation{ |
| 2 | public static void main(String[] args){ |
| 3 | add(); |
| 4 | } |
| 5 | public void add() throws Exception{ |
| 6 | addition(); |
| 7 | } |
| 8 | } |
Q.36- Explain about Exception Propagation.
Ans: Exception is first thrown from the method which is at the top of the stack. If it doesn’t catch, then it pops up the method and moves to the previous method and so on until they are got.
This is called Exception propagation.
Example:
| 1 | public class Manipulation{ |
| 2 | public static void main(String[] args){ |
| 3 | add(); |
| 4 | } |
| 5 | public void add(){ |
| 6 | addition(); |
| 7 | } |
From the above example, the stack looks like as shown below:

If an exception occurred in the addition() method is not caught, then it moves to the method add(). Then it is moved to the main() method and then it will stop the flow of execution. It is called Exception Propagation.
Q.37- What is the final keyword in Java?
Ans:
Final variable:
Once a variable is declared as final, then the value of the variable could not be changed. It is like a constant.
Example:
final int = 12;
Final method:
A final keyword in a method that couldn’t be overridden. If a method is marked as a final, then it can’t be overridden by the subclass.
Final class:
If a class is declared as final, then the class couldn’t be subclassed. No class can extend the final class.
Q.38- What is a Thread?
Ans: In Java, the flow of a execution is called Thread. Every java program has at least one thread called main thread, the Main thread is created by JVM. The user can define their own threads by extending Thread class (or) by implementing Runnable interface. Threads are executed concurrently.
Example:
| 1 | public static void main(String[] args){//main thread starts here |
| 2 | } |
Q.39- How do you make a thread in Java?
Ans: There are two ways available in order to make a thread.
#1) Extend Thread class:
Extending a Thread class and override the run method. The thread is available in java.lang.thread.
Example:
| 1 | Public class Addition extends Thread { |
| 2 | public void run () { |
| 3 | } |
| 4 | } |
The disadvantage of using a thread class is that we cannot extend any other classes because we have already extend the thread class. We can overload the run () method in our class.
#2) Implement Runnable interface:
Another way is implementing the runnable interface. For that we should provide the implementation for run () method which is defined in the interface.
Example:
| 1 | public static void main (String[] args){ |
| 2 | Thread t = new Thread (); |
| 3 | t.start (); |
| 4 | t.join (); |
| 5 | } |
From the above code, the main thread started the execution. When it reaches the code t.start() then ‘thread t’ starts the own stack for the execution. JVM switches between the main thread and ‘thread t’.
Once it reaches the code t.join() then ‘thread t’ alone is executed and completes its task, then only main thread started the execution.
It is a non-static method. Join () method has overloaded version. So we can mention the time duration in join () method also “.s”.
Q.40- What does yield method of the Thread class do?
Ans: A yield () method moves the currently running thread to a runnable state and allows the other threads for execution. So that equal priority threads have a chance to run. It is a static method. It doesn’t release any lock.
Yield () method moves the thread back to the Runnable state only, and not the thread to sleep (), wait () (or) block.
Example:
| 1 | public static void main (String[] args){ |
| 2 | Thread t = new Thread (); |
| 3 | t.start (); |
| 4 | } |
| 5 | public void run(){ |
| 6 | Thread.yield(); |
| 7 | } |
| 8 | } |
Q.41- Explain about wait () method.
Ans: wait () method is used to make the thread to wait in the waiting pool. When a wait () method is executed during a thread execution then immediately the thread gives up the lock on the object and goes to the waiting pool. Wait () method tells the thread to wait for a given amount of time.
Then the thread will wake up after notify () (or) notify all () method is called.
Wait() and the other above-mentioned methods do not give the lock on the object immediately until the currently executing thread completes the synchronized code. It is mostly used in synchronization.
Example:
| 1 | public static void main (String[] args){ |
| 2 | Thread t = new Thread (); |
| 3 | t.start (); |
| 4 | Synchronized (t) { |
| 5 | Wait(); |
| 6 | } |
| 7 | } |
Q.42- Difference between notify() method and notifyAll() method in Java.
Ans: Given below are few differences between notify() method and notifyAll() method
| notify() | notifyAll() |
| This method is used to send a signal to wake up a single thread in the waiting pool. | This method sends the signal to wake up all the threads in a waiting spool. |
Q.43- How to stop a thread in java? Explain about sleep () method in a thread?
Ans: We can stop a thread by using the following thread methods.
- Sleeping
- Waiting
- Blocked
Sleep:
Sleep () method is used to sleep the currently executing thread for the given amount of time. Once the thread is wake up it can move to the runnable state. So sleep () method is used to delay the execution for some period.
It is a static method.
Example:
Thread. Sleep (2000)
So it delays the thread to sleep 2 milliseconds. Sleep () method throws an uninterrupted exception, hence we need to surround the block with try/catch.
| 1 | public class ExampleThread implements Runnable{ |
| 2 | public static void main (String[] args){ |
| 3 | Thread t = new Thread (); |
| 4 | t.start (); |
| 5 | } |
| 6 | public void run(){ |
| 7 | try{ |
| 8 | Thread.sleep(2000); |
| 9 | }catch(InterruptedException e){ |
| 10 | } |
| 11 | } |
Q.44- When to use Runnable interface Vs Thread class in Java?
Ans: If we need our class to extend some other classes other than the thread then we can go with the runnable interface because in java we can extend only one class.
If we are not going to extend any class then we can extend the thread class.
Q.45- Difference between start() and run() method of thread class.
Ans: Start() method creates new thread and the code inside the run () method is executed in the new thread. If we directly called the run() method then a new thread is not created and the currently executing thread will continue to execute the run() method.
Q.46- What is Multi-threading?
Ans: Multiple threads are executed simultaneously. Each thread starts their own stack based on the flow (or) priority of the threads.
Example Program:
| 1 | public class MultipleThreads implements Runnable |
| 2 | { |
| 3 | public static void main (String[] args){//Main thread starts here |
| 4 | Runnable r = new runnable (); |
| 5 | Thread t=new thread (); |
| 6 | t.start ();//User thread starts here |
| 7 | Addition add=new addition (); |
| 8 | } |
| 9 | public void run(){ |
| 10 | go(); |
| 11 | }//User thread ends here |
| 12 | } |
On the 1st line execution, JVM calls the main method and the main thread stack looks as shown below.

Once the execution reaches, t.start () line then a new thread is created and the new stack for the thread is also created. Now JVM switches to the new thread and the main thread are back to the runnable state.
The two stacks look as shown below.
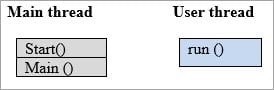
Now, the user thread executed the code inside the run() method.

Once the run() method has completed, then JVM switches back to the main thread and the User thread has completed the task and the stack was disappeared.
JVM switches between each thread until both the threads are completed. This is called Multi-threading.
Q.47- Explain the thread life cycle in Java.
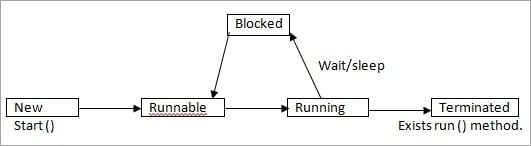
Ans: Thread has the following states:
- New
- Runnable
- Running
- Non-runnable (Blocked)
- Terminated
- New:
In New state, Thread instance has been created but start () method is not yet invoked. Now the thread is not considered alive.
- Runnable:
The Thread is in runnable state after invocation of the start () method, but before the run () method is invoked. But a thread can also return to the runnable state from waiting/sleeping. In this state the thread is considered alive.
- Running:
The thread is in running state after it calls the run () method. Now the thread begins the execution.
- Non-Runnable(Blocked):
The thread is alive but it is not eligible to run. It is not in runnable state but also, it will return to runnable state after some time.
Example: wait, sleep, block.
- Terminated :
Once the run method is completed then it is terminated. Now the thread is not alive.
Q.48- What is Synchronization?
Ans: Synchronization makes only one thread to access a block of code at a time. If multiple thread accesses the block of code, then there is a chance for inaccurate results at the end. To avoid this issue, we can provide synchronization for the sensitive block of codes.
The synchronized keyword means that a thread needs a key in order to access the synchronized code.
Locks are per objects. Every Java object has a lock. A lock has only one key. A thread can access a synchronized method only if the thread can get the key to the objects lock.
For this, we use “Synchronized” keyword.
Example:
public class ExampleThread implements Runnable{public static void main (String[] args){ Thread t = new Thread (); t.start (); } public void run(){ synchronized(object){ { }}
Q.49- What is the disadvantage of Synchronization?
Ans: Synchronization is not recommended to implement all the methods. Because if one thread accesses the synchronized code then the next thread should have to wait. So it makes slow performance on the other end.
Q.50- What is meant by Serialization?
Ans: Converting a file into a byte stream is known as Serialization. The objects in the file is converted to the bytes for security purposes. For this, we need to implement java.io.Serializable interface. It has no method to define.
Variables that are marked as transient will not be a part of the serialization. So, we can skip the serialization for the variables in the file by using a transient keyword.
Q.51- What is the purpose of a transient variable?
Ans: Transient variables are not part of the serialization process. During deserialization, the transient variables values are set to default value. It is not used with static variables.
Example:
transient int numbers;
Q.52- Which methods are used during the Serialization and Deserialization process?
Ans: ObjectOutputStream and ObjectInputStream classes are higher level java.io. package. We will use them with lower level classes FileOutputStream and FileInputStream.
ObjectOutputStream.writeObject —->Serialize the object and write the serialized object to a file.
ObjectInputStream.readObject —> Reads the file and deserializes the object.
To be serialized, an object must implement the serializable interface. If superclass implements Serializable, then the subclass will automatically be serializable.
Q.53 What is the purpose of a Volatile Variable?
Ans: Volatile variable values are always read from the main memory and not from thread’s cache memory. This is used mainly during synchronization. It is applicable only for variables.
Example:
volatile int number;
Q.54 Difference between Serialization and Deserialization in Java.
Ans: These are the difference between serialization and deserialization in java:
| Serialization | Deserialization |
| Serialization is the process which is used to convert the objects into byte stream | Deserialization is the opposite process of serialization where we can get the objects back from the byte stream. |
| An object is serialized by writing it an ObjectOutputStream. | An object is deserialized by reading it from an ObjectInputStream. |
Q.55- What is SerialVersionUID?
Ans: Whenever an object is Serialized, the object is stamped with a version ID number for the object class. This ID is called the SerialVersionUID. This is used during deserialization to verify that the sender and receiver that are compatible with the Serialization.